Hello, math wizzes! I am in need of your assistance. In the spoilers you'll find pictures of problems that I'm having issues getting the answers to and would love if you could either point me in the right direction or identify whatever error I may be making, or possibly even both.
Converting to polar coordinates:
Spoiler
Now, for this one it looks like I'm going to be doing a trig substitution, but I can't seem to get past that last line since I can't do a u-sub with what I'm given. I don't think I made a mistake anywhere, but me making a mistake is definitely not unheard of.
Finding mass and center of mass of a lamina over a region:
1:
Spoiler
For this one, I'm not entirely sure what my limits are supposed to be, at least for theta. We have an example from class that used the hypotenuse of one triangle as the upper limit of theta, and the x-axis was the lower limit (i.e. 0 <= theta <= upper limit). I'm also somewhat certain that the limit for r is supposed to go from 0 to 2sec(theta) (by setting 2 = rcos(theta)) but I may be wrong for that, too. At first I didn't convert to polar and just plugged and chugged by integrating w.r.t y and then x, but got no where near the answer of 54.
2:
Spoiler
For this one, I mat just plain have the limits wrong or am doing something wrong in the integration, and possible both. I've done it twice and have gotten the same answer, which is not the answer I'm supposed to be getting.
If anyone could help me out with these issues and possibly teach me some general tricks I could apply to other problems I would greatly appreciate it.
Oh, and hopefully you can read my handwriting. I know that sometimes it can get a bit messy.



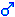





 Reply With Quote
Reply With Quote



 about this post
about this post


Bookmarks